Small-scale proxies

Introduction

LLMs show instabilities which either:

Slow learning

Destabilize learning

Appear to be focusing on instabilities which lead to slow divergence, not loss spikes.

We find that measuring the relationship between learning rate and loss across scales is a useful tool to identify instability

Based on this, they introduce concept of “LR sensitivity” measuring:

deviation from optimal performance when varying LR

Key aim is to demonstrate sources of LLM instability for SMLs. They do this by using high LRs for small models.

This then lets them show at a small scale the issues of:

growth of logits in attention layers

divergence of the output logits from the log probabilities

This further enables comprehensive analysis of interventions designed to mitigate these problems:

qk-layernorm

z-loss regularisation

These are shown to reduce the LR sensitivity (our proxy metric) which is then shown to enable stable training at scale.

Follow-up question: how do other common model(/optimiser) modifications affect scaling?

Examine:

warm-up

weight decay

µParam

Experimental methodology

Set-up

GPT-2 style models (pre-norm)

AdamW (0.9, 0.95, e=1e-8)

Gradient clipping (at norm 1)

5% warmup (100k updates; linear up, cosine down)

No embedding sharing

No biases (from PALM: “We found this to result in increased training stability for large models”)

Rope embeddings

Trained on C4

Init = TruncNorm(0, 1/sqrt(fan_in)), except embedding, which is 1/sqrt(d)

Batch size = 256

Seq len = 512

Vocab size = 32K

bfloat16 precision

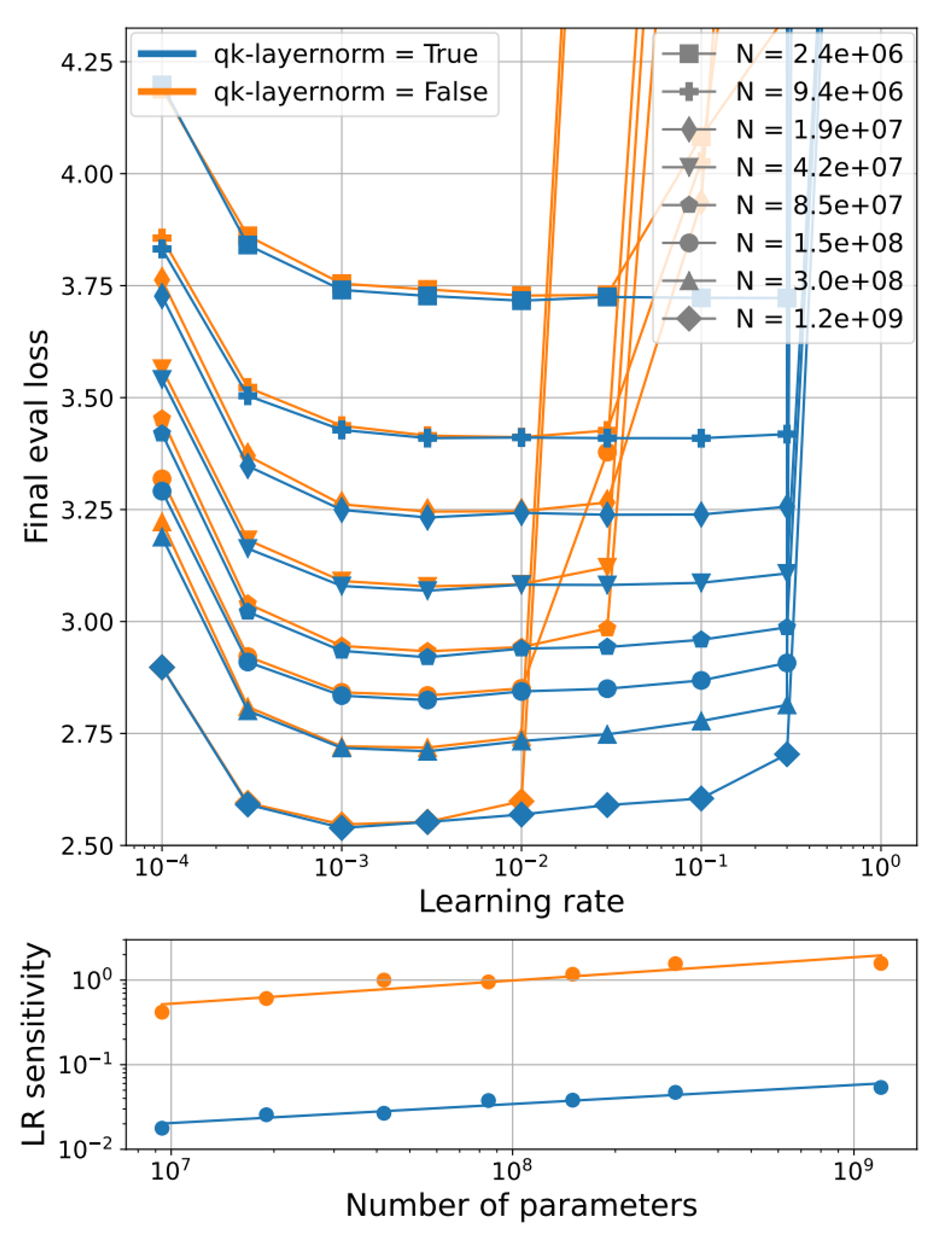
LR sensitivity

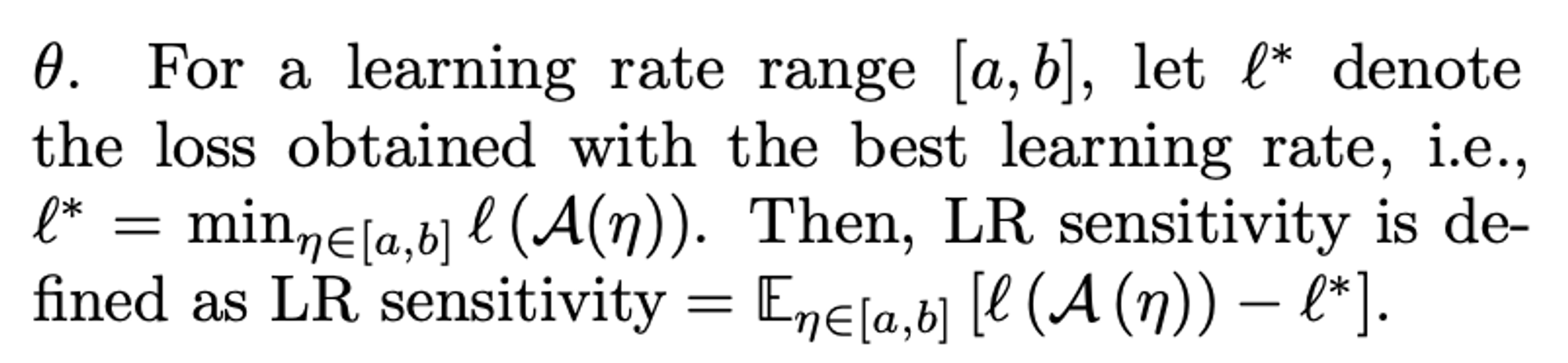
How should you choose a & b? Relative to the best LR somehow?

They just use the range 3e-4 to 3e-1.

The point is just that when you go over the max LR you shouldn’t explode. So perhaps the exact range doesn’t matter too much.

Results

Reproducing two known LLM instabilities for SLMs

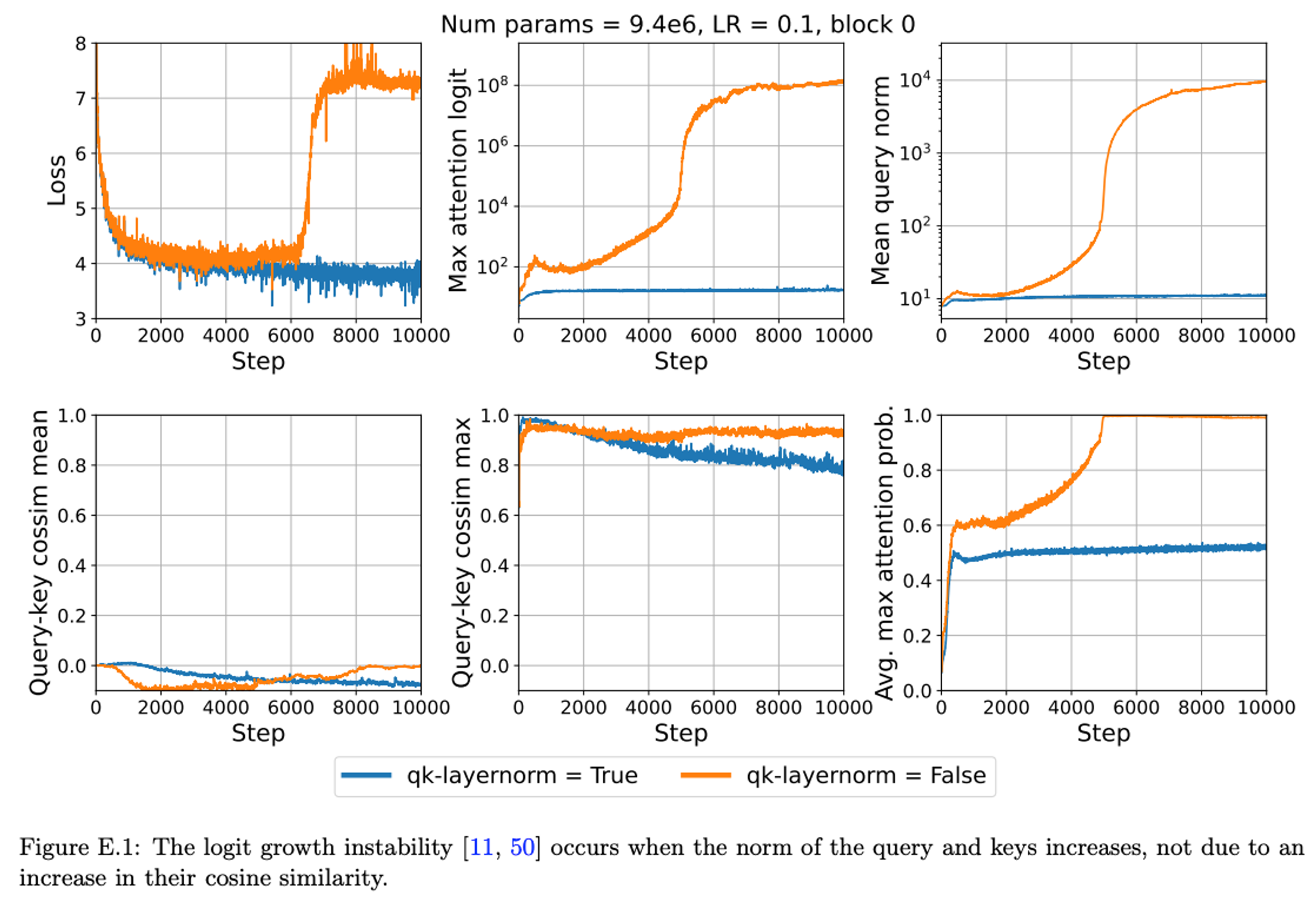
Firstly the growth of attention logits:

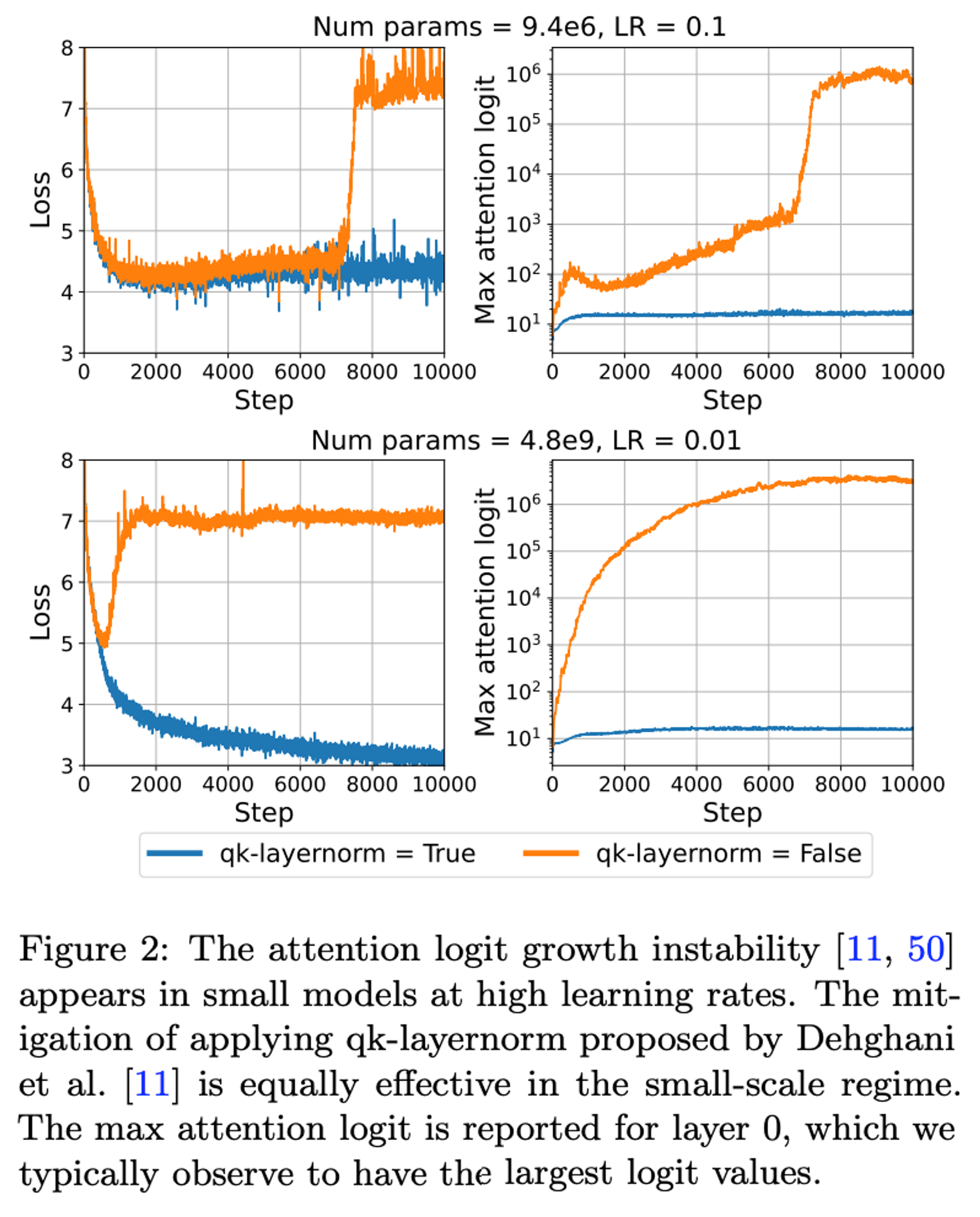
This shows that for the SLM the same issue comes up as the LLM if you increase the learning rate.

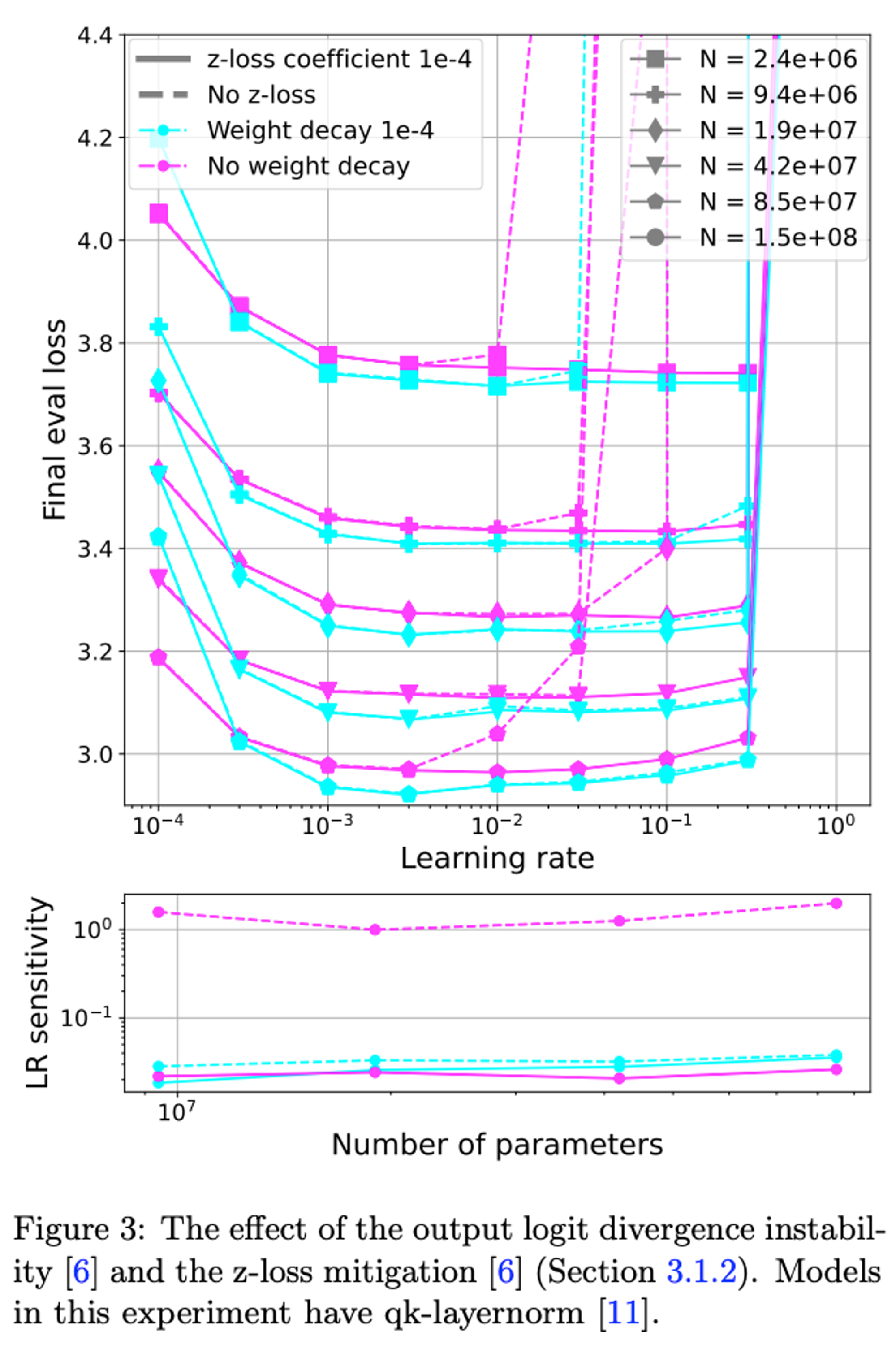
A solution (from the 22B ViT paper):

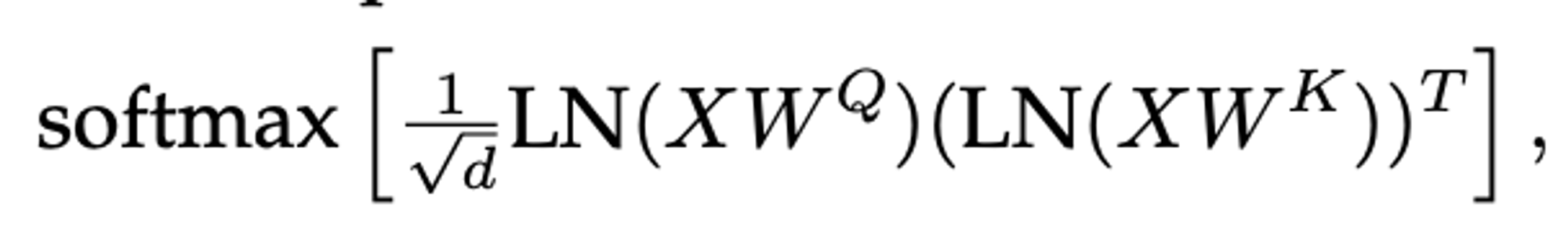
When this is applied the explosion in large LRs for the small model now only applies to very large LRs. The LR sensitivity plot below reflects this concisely.

The blow-up in attn logits could either be due to cosine-similarity, or the size of the queries & keys themselves. Results show it’s the latter:

Secondly the growth in output-layer logits:

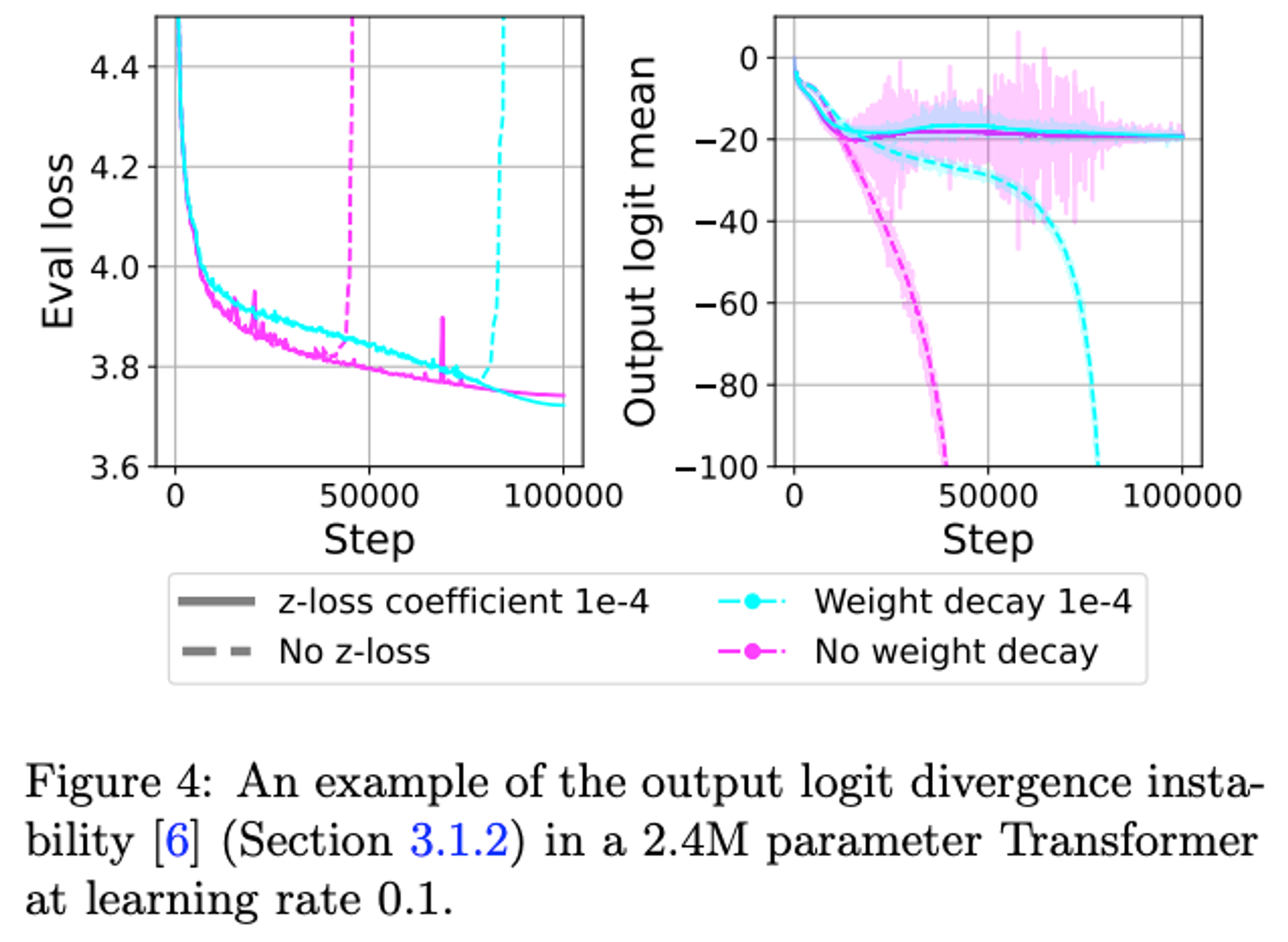
The loss they add is log^2(Z) where Z = sum(e^y_i) and y is the output of the final layer.

My mental model of how this works is that the standard loss is

Where . This is minimised when , although practically it can only reach 0. This happens when all the s are . The additional loss term of is minimised when → a much more numerically sensible position!

Note that “weight decay also mitigates this instability for the larger models we test”, so this might not be as much of an issue.

Questions:

Attention logits:

Isn’t there some alternative trick to stop the attn logits growing in the first place? The layernorm seems like mitigation, not a cure.

What about key norm plots?